Using symmetric key cryptography, we are able to safely encrypt data and communications. We are even able to authenticate messages using MAC functions. But there is a problem: if we want to securely communicate with another person, we need to share a secret with that person. This is known as the key exchange problem: how can we agree with another person upon a secret key to use to encrypt our communications? In an ideal scenario, two people would meet in a safe place and choose together a key to be used to protect future communications. But this is often infeasible in practice. Think about establishing an encrypted connection with a website: you would need to meet in person with the system administrators for all the websites you would like to visit. Public key cryptography solves this problem by using two keys: a public key that is used to encrypt messages and a corresponding private key that is used to decrypt them. Once a message is encrypted using a public key, only the corresponding private key can decrypt them. So you can put your public key in a public place or send it to another person using a public channel, and the messages encrypted with that key and then sent to you will be secure as long as you keep your private key safe.
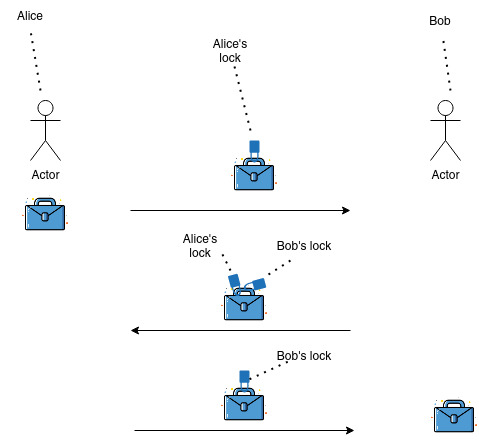
But how can we obtain a scheme where we have two keys, one used to encrypt data and another to decrypt it? Historically, while trying to solve this problem cryptographers had the following real-world analogy in mind. Let’s say that Alice wants to send a message to Bob. Bob owns an ideal briefcase, that can be locked, and once locked the only way of opening it is to open its lock. Both Alice and Bob own an ideal lock. Such a lock can be opened only by possessing the corresponding key. Those keys are ideal too, meaning that they can’t be forged or cloned. (Feel free to add any hypothesis that I might have missed, the idea here is that to open a lock there is no way except possessing the corresponding key). In this analogy, the public key is the briefcase and a lock, while the private key is the lock’s key. How can Alice use those tools to securely send a message to Bob? Feel free to stop here for a while and try to solve this yourself. You’ll see the solution below.
Hint
The briefcase can be locked with multiple locks.
Here’s the solution: Alice gets Bob’s briefcase. She then writes her message on a piece of paper, puts it inside the briefcase and locks it with her lock. She then ships the briefcase to Bob. The briefcase can’t be opened in transit as it is locked with Alice’s lock. When Bob receives it, he can’t open it as he doesn’t have Alice’s key, but he can lock it using his own lock and ship it back to Alice. Now the briefcase can’t be opened in transit as it is locked with both Alice’s and Bob’s locks. When Alice gets it back, she can remove her lock and ship it back to Bob. The message is still protected, as the briefcase is still locked with Bob’s lock. Finally, when Bob receives it he can open his lock using his own key and read the message.
You may have noticed that so far we didn’t mention authentication. A crucial part of secure communication is making sure that you are indeed sending messages to the correct person. For this, we need some way of authenticating the public keys. This is a problem independent of which public key cryptography scheme we are using, and will be explained separately.
This is all for now, we will see an actual public key scheme in the next article. See you!